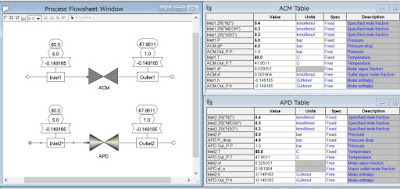
This is a simple membrane reactor model described in a textbook.
H. Scott Fogler (2010), Section 6.4 Membrane Reactors,
Essentials of Chemical Reaction Engineering, p.p. 217-225
In the textbook, specific components were not specified.
So, I treated the reaction as propane dehydrogenation.
i.e. C3H8 (Propane) -> C3H6 (Propylene) + H2
In this example, heat duty was also calculated.
ACM is very convenient for user to consider the heat balance.
Because molar enthalpy can be taken with a single line as below.
Call (hret) = pEnth_Mol_Vap(T, P, zret) ;
Download ACM file (V8.8)
Download MSI file (V8.8)
Download Aspen Plus file (V8.8)
Model MembReactor
Kc As RealVariable
(Description:"Equilibrium constant [mol/dm3]", Fixed, 0.05);
k As RealVariable
(Description:"Reaction rate constant [1/min]", Fixed, 0.7);
Cto As RealVariable
(Description:"Total molar concentration [mol/dm3]");
kc_ As RealVariable
(Description:"Transport coefficient [1/min]" , Fixed, 0.2);
V As LengthDomain (DiscretizationMethod:"OCFE4",
HighestOrderDerivative:1,
Length:500,
NumSections:2,
SpacingPreference:5,
Section(2).Location:100,
Section(2).SpacingPreference:20);
Fa As Distribution1D(XDomain Is V, HighestOrderXDerivative:1)
Of RealVariable(0); // [mol/min]
Fb As Distribution1D(XDomain Is V, HighestOrderXDerivative:1)
Of RealVariable(0); // [mol/min]
Fc As Distribution1D(XDomain Is V, HighestOrderXDerivative:1)
Of RealVariable(0); // [mol/min]
Nodes As IntegerSet([0 + V.Interior + V.EndNode]);
Ft(Nodes) As RealVariable; // [mol/min]
ra(Nodes) As RealVariable;
T As temperature;
P As pressure;
Q As enthflow;
// Inlet variables
Fin As RealVariable; // [mol/min]
zin(Componentlist) As molefraction;
hin As enth_mol;
Vin As vol_mol;
MWin As molweight;
// Retentate variables
Fret As RealVariable; // [mol/min]
zret(Componentlist) As molefraction;
hret As enth_mol;
rhoVret As dens_mol;
Vret As vol_mol;
MWret As molweight;
// Permeate variables
Fper As RealVariable; // [mol/min]
zper(Componentlist) As molefraction;
hper As enth_mol;
rhoVper As dens_mol;
Vper As vol_mol;
MWper As molweight;
// Ports
PortIn As Input MaterialPort;
PortRet As Output MaterialPort;
PortPer As Output MaterialPort;
// Inlet condition
PortIn.F = Fin / 1000 * 60 ;
PortIn.T = T ;
PortIn.P = P ;
PortIn.z = zin ;
PortIn.h = hin ;
PortIn.V = Vin ;
Cto = 1 / Vin ;
// Boundary condition (Inlet)
Fa(0) = Fin * zin("A") ;
Fb(0) = Fin * zin("B") ;
Fc(0) = Fin * zin("C") ;
// Component mole balances
For i In [V.Interior + V.EndNode] Do
Fa(i).ddx = -ra(i) ;
Fb(i).ddx = ra(i) - kc_ * Cto * (Fb(i)/Ft(i)) ;
Fc(i).ddx = ra(i) ;
EndFor
// Total molar flow
Ft = Fa + Fb + Fc ;
// Reaction rate
ra = k * Cto * ((Fa/Ft) - Cto/Kc * (Fb/Ft) * (Fc/Ft)) ;
// Average molar weight
Call (MWin) = pMolWeight(zin) ;
Call (MWret) = pMolWeight(zret) ;
Call (MWper) = pMolWeight(zper) ;
// Specific Vapor Molar Enthalpy
Call (hret) = pEnth_Mol_Vap(T, P, zret) ;
Call (hper) = pEnth_Mol_Vap(T, P, zper) ;
// Specific Vapor Molar Density
Call (rhoVret) = pDens_Mol_Vap(T, P, zret) ;
Call (rhoVper) = pDens_Mol_Vap(T, P, zper) ;
// Mass Balance
Fin * MWin = Fret * MWret + Fper * MWper ;
// Heat Balance
Fin * hin + Q * 1000 / 60 = Fret * hret + Fper * hper ;
// Retentate condition
Fret = Ft(V.EndNode) ;
zret("A") = Fa(V.EndNode)/Ft(V.EndNode) ;
zret("B") = Fb(V.EndNode)/Ft(V.EndNode) ;
zret("C") = Fc(V.EndNode)/Ft(V.EndNode) ;
Vret = 1 / rhoVret ;
PortRet.F = Fret / 1000 * 60 ;
PortRet.T = T ;
PortRet.P = P ;
PortRet.z = zret ;
PortRet.h = hret ;
PortRet.V = Vret ;
PortRet.Av= 1 ;
// Permeate condition
zper("A") = 0 ;
zper("B") = 1 ;
zper("C") = 0 ;
Vper = 1 / rhoVper ;
PortPer.F = Fper / 1000 * 60 ;
PortPer.T = T ;
PortPer.P = P ;
PortPer.z = zper ;
PortPer.h = hper ;
PortPer.V = Vper ;
PortPer.Av= 1 ;
End
Example 6-2 Results (textbook)
Same results were obtained using ACM.
Heat duty was validated using Aspen Plus.